Probability can do strange things to your mind. This week I had a probability problem where every time I tried to use intuition to solve it I ended up going completely wrong. I thought I’d share it as I think it’s interesting.
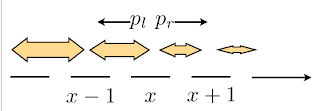
Consider a one dimensional random walk. At each time step my walker will go left with probability \(p_l\), and right with probability \(p_r\). It stays where it is with probability \(1 - p_l - p_r\). Furthermore these probabilities are dependent on the walker’s position in space, so it’s really \(p_l(x)\) and \(p_r(x)\). I’m imagining I’m on a finite line of length, L, although it doesn’t matter too much.
Now if \(p_l(x) = p_r(x) = \mathrm{constant} \), then we just have a normal random walker. In my problem I have the following setup: \(p_l(x) > p_r(x)\) but \(p_l(x+1) = p_r(x)\). What does this mean? At any given point, x, my walker is more likely to go left than right. If it does go left it will come back with the same rate (although it’s more likely to go left again).
So here’s the question: If I leave this for a really long time, what is the equilibrium probability distribution for the walkers position, \(P(x)\)?
Intuitive answer (1)
At any given site the chances are you are more likely to go left than
right. Therefore, this introduces a bias to go left. The walker is more
likely to be on the left hand side of the line after a long time.
Intuitive answer (2)
Because the transition rates are much faster on the left than the right,
if the walker happens to go to the left it will much more quickly
return. If the walker happens to go right then it’s going to take a long
time to return. Therefore you’re more likely to find it on the right.
The correct answer
Well it’s a little of both. The correct answer is that there is equal
probability of finding the walker absolutely anywhere. The reason for
this does not come from intuition. At equilibrium we have the condition
that there must be no probability “current”. That is to say that the
probability of being found at a given site must not change in time. This
can be expressed mathematically by the master equation (if you don’t
want to do the maths we’ll meet back at the end):
$$ \begin{aligned} \frac{\partial P(x)}{\partial t} &=& P(x + 1)p_l(x + 1) + P(x - 1)p_r(x - 1) && -P(x)(p_l(x) + p_r(x)) \end{aligned} $$
You have to think of the ps as rates for this to work. In our case we have that the rate for going left or right is the same as making the reverse move. The master equation then reduces to
$$ p_r(x-1) \big[ P(x-1) - P(x) \big] = p_r(x) \big[ P(x) - P(x + 1) \big] $$
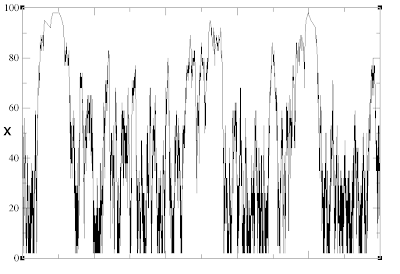
and the solution is that \(P(x) = \mathrm{constant} = 1/L\). So how does this sit with our intuitive ideas above? Well perhaps it’s best to look at a trace of such a random walk. In the below example we have that \( p_r(x) \big( 1 - x / (L+1) \big)^2 \). What happens is that the walker does indeed move quickly at small x and slowly at large x (as in intuitive answer 2), but the slowness at large x seems to reflect the walker away. When it does manage to penetrate the barrier it takes a long time to come back. The average behaviour is that every site, x, is occupied for the same amount of time.
So there it is. Never trust your instincts when it comes to probability, well not mine at least.
Oh, and on a separate note, putting maths into a blog post is a bloody nightmare - any ideas?
UPDATE: Now have katex. It’s pretty neat.