While I was putting together the post on 2D disks I came across a lovely paper from 1962 on 2D melting by Alder and Wainwright. From there I found this paper from 1959: Studies in Molecular Dynamics. I. General Method by the same authors.
They describe the “event driven” molecular dynamics (MD) algorithm. Normally, with MD you calculate forces, and thus accelerations, and update this way. Hard disks or spheres behave more like snooker balls, the forces are more or less instantaneous impulses that conserve momentum so it’s better to deal with collision events and leave out the acceleration part.
The paper gives a fascinating insight into the early days of computer simulation (they still refer to them as “automatic computers”), what their limitations were and what details were worth worrying about. To give you an idea, in 1959 they say:
With the best presently available computers, it has been possible to treat up to five hundred molecules. With five hundred molecules it requires about a half-hour to achieve an average of one collision per molecule.
So in their case it was CPU speed that was the problem, they get about thousand collisions per hour. To put that in perspective, a modern event-driven simulation of a similar system will maybe hit about a billion collisions per hour on a reasonable desktop [source]. I don’t say this to mock their efforts, these are the giants on whom’s shoulders we stand. I’ll come back to why that number is so comparatively big these days, first I want to look at visualisation.
Visualistion
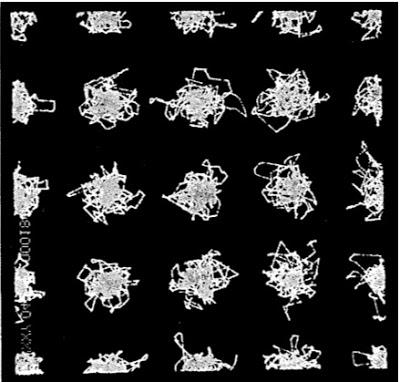
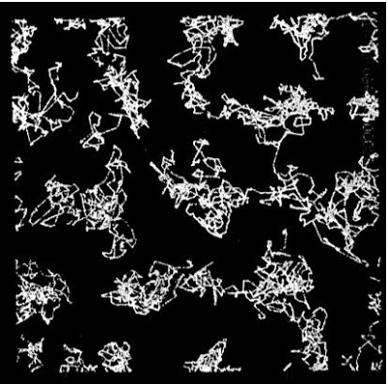
In 1959 there were no jpegs or postscripts and certainly no Povray or VMD, I’m not sure they even had printers. So how do you visualise your simulation? Well they had a rather elegant answer to that. They could output the current state of the system to a cathode-ray tube as a bunch of dots in the positions of the particles. Then they pointed a camera at the screen and left the shutter open while they ran a simulation. What you get is these beautiful images below showing the particle trajectories. Firstly in a crystal phase you can see the particles rattling around their lattice sites
This is a projection of the FCC lattice (the squares confused me at first). In the fluid phase they do a little bit of cage rattling and then start to wander off.
[Figures reprinted with permission Alder and Wainwright, J. Chem. Phys. 31, 459 (1959). Copyright 1959, American Institute of Physics].
I honestly couldn’t show it better today. Some people dismiss visualisations as pretty pictures that only exist to attract attention. Perhaps this is sometimes true but it only takes one look at this to see how they can stir the imagination and shape the intuition – and that’s what creates new ideas.
Algorithms
I’d quickly like to come back to the speed difference between 1959 and today. A lot of the difference can be put down to Moore’s law. After an annoying amount of Googling I can’t really say how much faster modern CPUs are. A lot probably. However, I’d like to focus on an often overlooked factor – the development of algorithms.
A general event driven algorithm calculates the collision time for each pair of particles and, if it is under a cutoff, stores it in an event queue. It then fast forwards to the shortest time whereupon it will need to update the queue with new events that appear after the collision. Initially this requires checking all pairs, Alder and Wainwright call this the “long cycle”, and this has complexity of order N-squared, O(N^2). This means that if you double the number of particles, N, then you have four times as many calculations to perform.
After a collision you only need to update events involving the particles that collided so you can get away with doing N updates. This is the “short cycle” and is O(N). It’s not mentioned in this paper but I think there’s an issue with sorting the event queue so this is probably still O(N^2). Either way, for their early simulations the total number of collisions per hour tanked as N was increased.
And this is where algorithms come in. You can use all sorts of tricks. In dense systems you can use a cell structure to rule out collisions between pairs far away. Modern algorithms focus largely on keeping the event queue properly sorted. A binary tree will sort with O(log(N)) and here they claim to have it O(1). Of course the complexity is not the only important factor, there may be other more important overheads, but it gives an idea of the limitations.
In equilibrium statistical mechanics specialised computer algorithms have made a spectacular impact. Techniques such as the Wolff algorithm, Umbrella sampling, and many many more, have outstripped any speed up by Moore’s law by many orders of magnitude. I could go on about algorithms for hours (maybe a post brewing), instead I’ll just make the point that it doesn’t always pay to just sit and wait for a faster computer.
We’ve come a long way
These early simulation studies weren’t just important for developing methods, they were able to answer some serious questions that were hopelessly out of reach at the time. Since then simulation has firmly established itself in the dance between theory and experiment, testing ideas and generating new ones. And it shows no sign of giving up that position.